Шифр магический квадрат — онлайн дешифровка
Магический квадрат — это уникальная математическая конструкция, представляющая собой квадратную таблицу размером n×n, заполненную натуральными числами от 1 до n² таким образом, что суммы чисел в каждой строке, каждом столбце и на обеих диагоналях равны одному и тому же значению.
Это значение называется «магической константой» и вычисляется по формуле:
M = n(n² + 1)/2
Например, для квадрата 3×3 магическая константа равна 15, для 4×4 — 34, для 5×5 — 65.
Шифр магический квадрат — это когда вы используя созданный по обозначенному выше правилу вписываете нужный текст в квадрат по порядку возрастания чисел, а затем итоговый текст просто списывается построчно построчно из квадрата.
Зашифровка и расшифровка шифра магический квадрат
Интуитивно понятный интерфейс, плюс отдельная вкладка на тот случай, если вам просто нужно сгенерировать квадрат с числами.
Магический квадрат — Шифратор/Дешифратор
Шифратор
Зашифрованный текст:
Дешифратор
Расшифрованный текст:
Генератор магических квадратов
Сгенерированный квадрат можно использовать для шифрования/дешифрования, переключившись на соответствующие вкладки.
История происхождения
Магические квадраты имеют богатую историю, уходящую корнями в древний Китай, где они считались обладающими мистической силой.
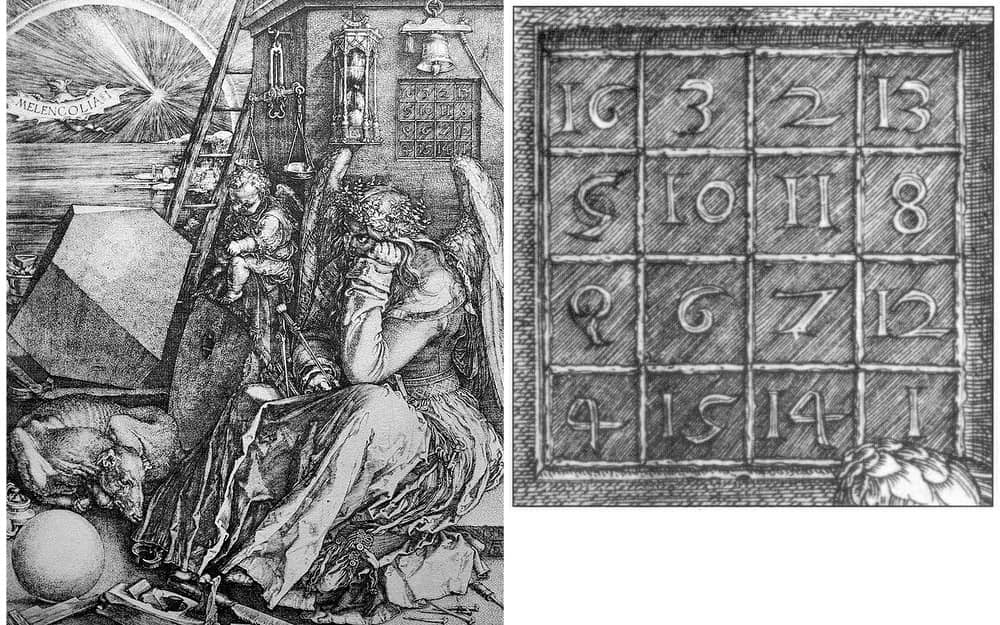
В Европе одним из самых известных примеров является магический квадрат 4×4, изображенный на гравюре Альбрехта Дюрера «Меланхолия» (1514 год).
Интересно, что два средних числа в нижнем ряду этого квадрата (15 и 14) образуют дату создания гравюры — 1514 год.
Типы магических квадратов
Они бывают следующих типов:
- Нормальный магический квадрат — содержит числа от 1 до n².
- Ассоциативный (симметричный) квадрат — сумма любых двух чисел, симметричных относительно центра, равна n² + 1.
- Пандиагональный квадрат — сохраняет магические свойства даже при «циклическом» переносе строк или столбцов.
Принцип шифрования магическим квадратом
- Выбор подходящего магического квадрата (размер определяется длиной сообщения).
- Нумерация букв исходного текста от 1 до n².
- Вписывание букв в квадрат согласно нумерации клеток.
- Считывание результата построчно слева направо для получения шифртекста.
Пример шифрования
Давайте подробно разберем процесс шифрования фразы «Я ИГРАЮ В КВЕСТЫ» с использованием магического квадрата
Шаг 1: Подготовка сообщения
- Удаляем пробелы: «ЯИГРАЮВКВЕСТЫ»
- Считаем количество букв: 11 символов
- Так как 11 не является квадратом целого числа, дополняем фразу нейтральными символами (например, «_») до ближайшего квадрата. Ближайший квадрат: 16 (4×4)
- Добавляем 5 символов «_»: «ЯИГРАЮВКВЕСТЫ_____»
Шаг 2: Выбор магического квадрата 4×4
Используем классический магический квадрат Дюрера:
| 16 | 3 | 2 | 13 |
| 5 | 10 | 11 | 8 |
| 9 | 6 | 7 | 12 |
| 4 | 15 | 14 | 1 |
Шаг 3: Заполнение квадрата буквами
Нумеруем буквы сообщения:
1-Я, 2-И, 3-Г, 4-Р, 5-А, 6-Ю, 7-В, 8-К, 9-В, 10-Е, 11-С, 12-Т, 13-Ы, 14-, 15-, 16-_
Заполняем квадрат:
| 16,_ | 3,Г | 2,И | 13,Ы |
| 5,А | 10,Е | 11,С | 8,К |
| 9,В | 6,Ю | 7,В | 12,Т |
| 4,Р | 15,_ | 14,_ | 1,Я |
Шаг 4: Получение шифртекста
Считываем буквы построчно, слева направо:
- Первая строка: _, Г, И, Ы → «_ГИЫ»
- Вторая строка: А, Е, С, К → «АЕСК»
- Третья строка: В, Ю, В, Т → «ВЮВТ»
- Четвертая строка: Р, _, _, Я → «Р__Я»
Объединяем: «_ГИЫ АЕСК ВЮВТ Р__Я«
Дешифровка шифра магический квадрат
Для этого произведем обратный процесс:
- Записываем шифртекст в квадрат 4×4:
| 16,_ | 3,Г | 2,И | 13,Ы |
| 5,А | 10,Е | 11,С | 8,К |
| 9,В | 6,Ю | 7,В | 12,Т |
| 4,Р | 15,_ | 14,_ | 1,Я |
- Читаем буквы в порядке номеров клеток (от 1 до 16):
Я 2. И 3. Г 4. Р 5. А 6. Ю 7. В 8. К 9. В 10. Е 11. С 12. Т 13. Ы 14. _ 15. _ 16. _
Важные замечания
Размер квадрата должен соответствовать длине сообщения (с дополнениями).
Для настоящей криптографии нужно:
- Использовать уникальный квадрат (не общеизвестный)
- Согласовать с получателем метод дополнения сообщения
- Возможно, добавить дополнительные уровни шифрования
Криптографические свойства
Преимущества:
- Простота реализации
- Большое количество возможных ключей (880 вариантов для 4×4, около 250000 для 5×5)
- В историческом контексте — дополнительная «магическая» защита
Недостатки:
- Сохраняет частотные характеристики языка
- Требует сообщения строго определенной длины (n² символов)
- При небольших n уязвим к полному перебору
Методы генерации магических квадратов
Магические квадраты можно генерировать различными способами в зависимости от их порядка (размера). Рассмотрим три основных метода построения магических квадратов.
Метод Сиама (для нечетных порядков)
Применение: Для квадратов с нечетной стороной (3×3, 5×5, 7×7 и т.д.)
Алгоритм построения:
- Начальная позиция: Поместите 1 в среднюю клетку верхней строки.
- Движение: Последующие числа размещаются по диагонали вверх-вправо.
Особые случаи:
- Если движение приводит за пределы квадрата сверху, продолжайте снизу
- Если движение приводит за пределы справа, продолжайте слева
- Если клетка уже занята, поместите число непосредственно под предыдущим числом
Пример для 3×3:
| 8 | 1 | 6 |
| 3 | 5 | 7 |
| 4 | 9 | 2 |
Метод Рауз-Болла (для порядков, кратных 4)
Применение: Для квадратов с размером, кратным 4 (4×4, 8×8, 12×12 и т.д.)
Алгоритм построения:
- Разделение на подквадраты: Разделите основной квадрат на блоки 4×4
- Заполнение диагоналей: В каждом блоке 4×4 выделите главные диагонали
Заполнение чисел:
- На диагоналях: n²+1-k (где k — текущее число)
- Вне диагоналей: обычная последовательность чисел
Пример для 4×4:
| 16 | 3 | 2 | 13 |
| 5 | 10 | 11 | 8 |
| 9 | 6 | 7 | 12 |
| 4 | 15 | 14 | 1 |
Основные особенности:
- Использует свойство дополнительности чисел
- Создает ассоциативные (симметричные) квадраты
- Хорошо подходит для больших размеров
Метод Лью Конуэя (для четно-нечетных порядков)
Применение: Для квадратов порядка n = 4k + 2 (6×6, 10×10, 14×14 и т.д.)
Алгоритм построения — прежде всего разделите квадрат на четыре равных квадранта.
Заполнение квадрантов:
- Левый верхний: квадрант A (порядок 2k+1) — заполняется методом Сиама
- Правый верхний: квадрант B = A + (2k+1)²
- Левый нижний: квадрант C = B + (2k+1)²
- Правый нижний: квадрант D = A + 3*(2k+1)²
В конце потребуется коррекция: поменяйте местами определенные элементы между квадрантами.
Пример для 6×6:
| 35 | 1 | 6 | 26 | 19 | 24 |
| 3 | 32 | 7 | 21 | 23 | 25 |
| 31 | 9 | 2 | 22 | 27 | 20 |
| 8 | 28 | 33 | 17 | 10 | 15 |
| 30 | 5 | 34 | 12 | 14 | 16 |
| 4 | 36 | 29 | 13 | 18 | 11 |
Особенности метода:
- Комбинирует подходы для нечетных и четных порядков
- Требует дополнительных корректировок после первоначального заполнения
- Создает нетривиальные магические квадраты
| Метод | Применимость | Сложность | Уникальность результата |
|---|---|---|---|
| Сиама | Нечетные порядки | Низкая | Один базовый вариант |
| Рауз-Болла | Кратные 4 | Средняя | Множество вариантов |
| Лью Конуэя | 4k+2 | Высокая | Множество вариантов |